多维(三维四维)矩阵向量运算-超强可视化
本文来源:【全面理解多维矩阵运算】多维(三维四维)矩阵向量运算-超强可视化 - 知乎 (zhihu.com)
作者:卓师叔,爱书爱金融的NLPer
微信公众号:卓师叔
注:高维矩阵或者向量的运算,是一个困扰着我很久的问题;在NLP里面经常就会碰到三维,四维的向量运算,矩阵相乘时相当头痛,比如著名的Attention中Q、K、V相乘,实在想不出来四维的到底长什么样,又是怎么相乘的。于是特地写下此文章,记录下个人的学习路程,也希望帮到大家。
1、高维矩阵可视化
一维: 首先一维的矩阵非常简单,比如[1,2,3,4],可以用下图表示

二维: 接着来看二维,可用以下代码生成一个二维矩阵,采用keras框架
import keras.backend as K
import numpy as np
a = K.constant(np.arange(1, 7), shape=[2,3])
print(K.eval(a))
输出为:
[[1. 2. 3.]
[4. 5. 6.]]
看维度的小技巧:想知道一个矩阵的维度是几维的,只需要看开头有几个“[”,有1个即为1维,上面的两个就是两维,后面举到的三维和四维的例子,分别是有三个“[”、四个“[”的。
上面这两维可视化长这样:
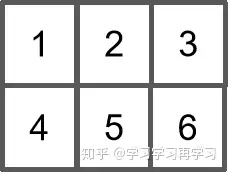
为了方便后续解释三维和四维,我们把它旋转一个小角度,如下
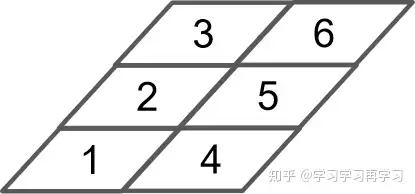
三维: 同样可用以下代码生成一个三维矩阵
a = K.constant(np.arange(1, 13), shape=[2,2,3])
print(K.eval(a))
输出为:
[[[ 1. 2. 3.]
[ 4. 5. 6.]]
[[ 7. 8. 9.]
[10. 11. 12.]]]
因为输出的结果有三个“[”,所以是三维的矩阵。这是一个shape=[2,2,3]的三维矩阵,可视化如下
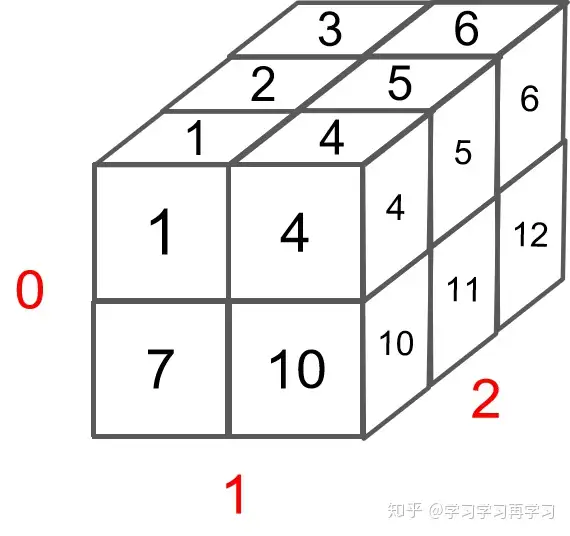
分片看一下!
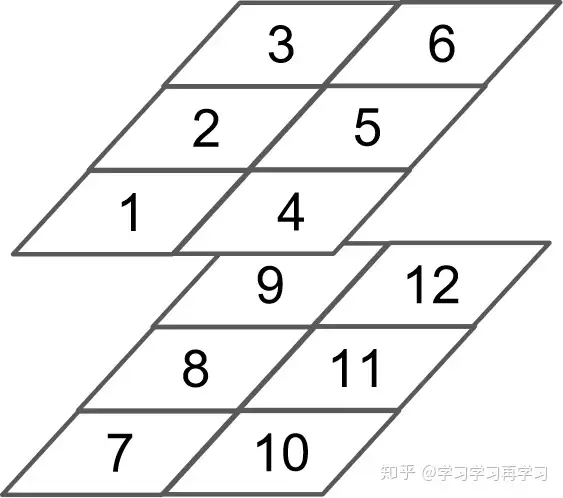
认真看数据的分布:三维的其实就类似于上面的二维堆起来后的样子,[[ 1. 2. 3.] [ 4. 5. 6.]]在上半部分,[[ 7. 8. 9.] [10. 11. 12.]]在下半部分,两个堆叠起来后就是最终三维的样子。
结论:shape=[2,2,3]的三维矩阵,可以视为2个shape=[2,3]的二维矩阵堆叠在一起!!最后两维才是有数据的矩阵,前面的维度只是矩阵的排列而已!
注意上图中 红色的0,1,2 ,表示的是输出的三个维度,在可视化中的位置。
总结怎么画三维:
先根据shape画出一个三维,shape=[2,2,3]分别对应着可视化中红色的0,1,2中小格子的个数
填充两维,在可视化中分别是1,2这两个维度上,把数据填充上,也就是上半部分的[[ 1. 2. 3.] [ 4. 5. 6.]]
填充剩余部分的[[ 7. 8. 9.] [10. 11. 12.]],并堆叠在一起形成三维。
所以以后一看到三维的,就马上想起这张图,后续很有用。
四维: 同样可用以下代码生成一个四维矩阵
a = K.constant(np.arange(1, 25), shape=[2,2,2,3])
print(K.eval(a))
输出为:
[[[[ 1. 2. 3.]
[ 4. 5. 6.]]
[[ 7. 8. 9.]
[10. 11. 12.]]]
[[[13. 14. 15.]
[16. 17. 18.]]
[[19. 20. 21.]
[22. 23. 24.]]]]
在我们理解了三维后,就可以很容易的四维
结论:shape=[2,2,2,3]的四维矩阵,可以视为2个shape=[2,2,3]的三维矩阵堆叠在一起!!然后三维的最后是用二维的堆叠组成的!!第一个2表示的是batchsize!!最后两维才是有数据的矩阵,前面的维度只是矩阵的排列而已!
长这样,就是2个三维的
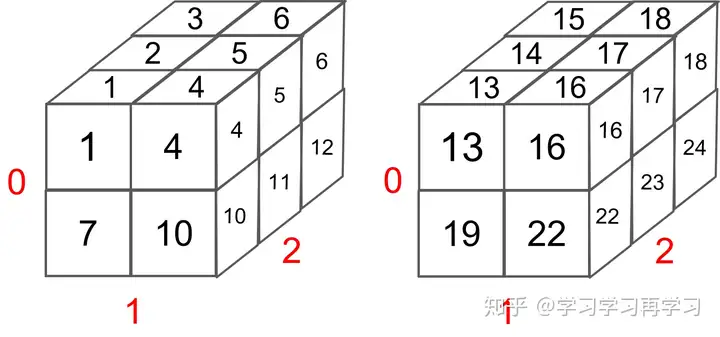
是不是很容易理解!
2、高维矩阵运算
从上面可以得出结论:所有大于二维的,最终都是以二维为基础堆叠在一起的!!
所以在矩阵运算的时候,其实最后都可以转成我们常见的二维矩阵运算,遵循的原则是:在多维矩阵相乘中,需最后两维满足shape匹配原则,最后两维才是有数据的矩阵,前面的维度只是矩阵的排列而已!
举个例子:比如两个三维的矩阵相乘,分别为shape=[2,2,3]和shape=[2,3,2]
a =
[[[ 1. 2. 3.]
[ 4. 5. 6.]]
[[ 7. 8. 9.]
[10. 11. 12.]]]
b =
[[[ 1. 2.]
[ 3. 4.]
[ 5. 6.]]
[[ 7. 8.]
[ 9. 10.]
[11. 12.]]]
上面说了,a可以表示成2个shape=[2,3]的矩阵,b可以表示成2个shape=[3,2]的矩阵,前面的额表示的是矩阵排列情况。
计算的时候把a的第一个shape=[2,3]的矩阵和b的第一个shape=[3,2]的矩阵相乘,得到的shape=[2,2],即
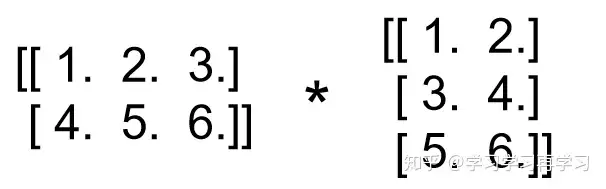
同理,再把a,b个字的第二个shape=[2,3]的矩阵相乘,得到的shape=[2,2]。
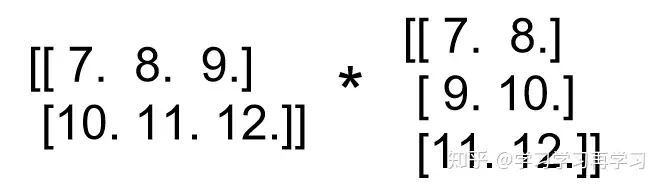
最终把结果堆叠在一起,就是2个shape=[2,2]的矩阵堆叠在一起,结果为:
[[[ 22. 28.]
[ 49. 64.]]
[[220. 244.]
[301. 334.]]]
也就是shape=[2,2,3]和shape=[2,3,2]矩阵相乘,最后答案的shape为:把第一维表示矩阵排情况的2,直接保留作为结果的第一维,再把后面两维的通过矩阵运算,得到shape=[2,2]的矩阵,合起来结果shape=[2,2,2]。
四维的同理!拆成多个三维矩阵来运算即可!!
需要注意的是,四维中, 前两维是矩阵排列,相乘的话保留前的最大值 。
比如a:shape=[2,1,4,5],b:shape=[1,1,5,4]相乘,输出的结果中,前两维保留的是[2,1],最终结果shape=[2,1,4,4]