Gaussian中用TDDFT计算激发态和吸收、荧光、磷光光谱的方法

本文引用自sob老师的博客： http://sobereva.com/314

1. 电子跃迁过程

实际上，吸收、发射过程既涉及到电子态的改变也涉及到振动态的改变，完整考虑这样的过程比较麻烦，需要优化基态结构、对基态做振动分析、优化激发态结构（挺耗时）、对激发态做振动分析（巨耗时）。

为了简化计算和讨论，人们一般忽略核振动的量子效应，只考虑电子势能面。此时电子跃迁可用以下假想模型表示：

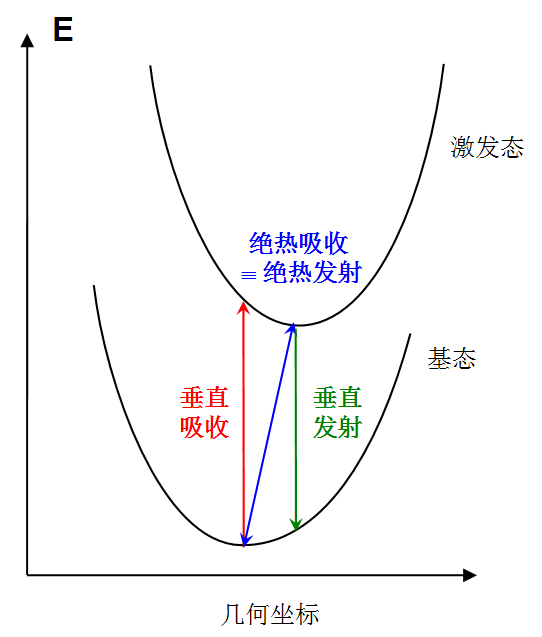
我们一般研究激发态计算的是以下三种理想化的跃迁方式：

(1)垂直吸收：电子从基态吸收光子而被激发到激发态，结构保持基态的极小点结构。计算垂直吸收能包含以下两步 1.优化基态几何结构 2.在1的结构下计算基态到感兴趣的激发态的激发能

(2)垂直发射：电子从激发态发射光子而退激到基态，结构保持激发态的极小点结构。计算垂直发射能包含以下两步 1.优化激发态几何结构（初猜结构无所谓，如果不知道激发态结构什么样，一般用基态极小点结构作为初猜结构） 2.在1的结构下计算基态到激发态的激发能（这便是这个激发态垂直发射到基态的能量）

(3)绝热吸收：电子从基态被激发到激发态，结构也从基态极小点结构变化到激发态极小点结构。计算绝热吸收能包含以下三步 1.优化基态几何结构，在最后一步得到基态极小点能量 2.优化激发态几何结构，在最后一步得到激发态极小点能量 3.将第二步得到的能量与第一步得到的能量求差值 绝热发射是绝热吸收的逆过程，跃迁能量相同。

以上跃迁方式是理想化的，对理论研究有用，对于研究实际问题也有用。实际吸收、发射光谱的最大峰位置一般分别比较接近于垂直吸收能和垂直发射能。而0-0跃迁，即两个电子态的振动基态间的跃迁能，比较接近于绝热激发能。

基态是单重态(S0)时，发射过程又分为两类：

(1)荧光发射：是从单重态激发态发射光子退激到基态。根据kasha规则，荧光发射多数情况是从S1（能量最低的单重态激发态）退激到S0。因此，按照上述垂直发射方式计算荧光的时候，激发态一般选的是S1态。少数情况kasha规则不满足，比如Azulene大多是从S2而非S1退激到S0的。

(2)磷光发射：是从三重态激发态发射光子退激到基态。磷光发射是从T1（能量最低的三重态激发态）退激到S0的。因此，按照上述垂直发射方式计算磷光的时候，激发态选的是T1态。

2. 跃迁电偶极矩与振子强度

假设初始态电子波函数为|i>，末态为|j>，则两个态之间的跃迁电偶极矩为<i|-r|j>。这里r是坐标矢量，负号是因为电子带负电荷。跃迁偶极矩一般指的就是跃迁电偶极矩，但也有跃迁磁偶极矩、跃迁速度偶极矩等等。注意，跃迁电偶极矩和两个态之间电偶极矩的差值，即<j|-r|j>-<i|-r|i>，根本没直接关系，很多初学者都搞混了。

有了跃迁电偶极矩和两个态能量差ΔE，就能得到两个态之间跃迁对应的振子强度f：(2/3)ΔE*|<i|-r|j>|^2，是个无量纲的量。

基态体系与某个激发态之间的振子强度越大，就越容易吸收相应频率的电磁波而跃迁到那个激发态上，因此吸收光谱中相应的吸收峰也越强。一般情况下振子强度小于1，但也完全可以大于1，极强吸收峰的振子强度甚至能达到接近7、8。振子强度小于0.01一般可以认为跃迁禁阻。

通过振子强度和两个态之间的能量差就可以根据爱因斯坦公式计算激发态寿命，对于荧光和磷光发射都适用，往往和实验对应得不错。如果和实验值差异很大，有可能发生了显著的内转换、外转换等无辐过程。计算公式为：寿命τ=1.5/(f*ΔE^2)。这里寿命的单位为秒，ΔE以cm-1为单位。寿命的倒数就是自发辐射速率。

三重态和单重态之间是自旋禁阻的，仅当考虑旋轨耦合时振子强度才不为零，但数值依然很小，所以磷光寿命远比荧光寿命长。

3. 电子光谱的产生

激发能、振子强度都是纯粹的理论数据，要把它转化为能和实验对比的UV-Vis（紫外-可见吸收光谱）、荧光、磷光光谱，需要把跃迁进行展宽。这里简单说一下计算过程。

(1)UV-Vis光谱：在基态优化的结构下计算基态到一批激发态的激发能和振子强度，然后把每个跃迁根据这两个量用高斯函数展宽，再把所有跃迁进行叠加，即得到UV-Vis光谱图。Gaussian等程序还顺便输出基态到各激发态的转子强度，用它代替振子强度进行展宽的话得到的是电子圆二色谱(ECD)。 (2)荧光光谱：假设kasha规则是满足的，在优化的S1结构下计算S1->S0的垂直发射能以及对应的振子强度，然后用高斯函数展宽成峰形即是荧光光谱图。 (3)磷光光谱：在优化的T1结构下计算T1->S0的垂直发射能以及对应的振子强度（需考虑旋轨耦合，否则必为0），然后用高斯函数展宽成峰形即是磷光光谱图。

至于展宽的细节和实现，详见前述的《使用Multiwfn绘制红外、拉曼、UV-Vis、ECD和VCD光谱图》。

由于电子激发实际上还涉及到不同振动态之间的跃迁，所以电子光谱是有精细结构的（但在极性溶剂下观测不到，只能观测到带状光谱）。如果不考虑核振动，即用前面介绍的计算方式，得到的理论光谱是没有精细结构的，特别是荧光、磷光光谱图上仅仅只有一个高斯峰形而已。如果要得到含有精细结构的电子光谱，即振动分辨（Vibrationally-resolved）的电子光谱，必须考虑核振动波函数。具体做法见前述的《振动分辨的电子光谱的计算》。算这个的成本比前述不考虑核振动效应时高得多。

4. 溶剂效应

溶剂效应对激发态的影响有多方面，会影响激发能而导致谱峰位移，还会影响吸收/发射的强度、使谱峰加宽和变形、影响激发态结构、出现外转换而退激等等。凡是实际是在溶液中发生的和电子激发有关的问题，计算时应当考虑溶剂，溶剂极性越强考虑的必要性越大。

量化计算激发能的时候一般都是用隐式溶剂模型，将溶剂环境当成具有一定介电常数的连续介质来考虑。这种方式考虑溶剂效应一般可以基本合理表现出它对激发能、振子强度的影响以及对激发态结构的影响。隐式溶剂模型种类很多，激发态计算的目的一般就用PCM，这也是Gaussian的SCRF关键词默认的，其它程序有的只支持比PCM形式更简单的COSMO，效果也差不多。

TDDFT级别下，隐式溶剂模型的溶剂场对激发态的响应有不同考虑方式。常用的有两种： (1)线性响应(Linear response, LR)：溶剂对激发能的修正量是跃迁密度与跃迁密度导致的溶剂极化之间的相互作用。这种处理比较常用，相比气相计算不会额外带来太多耗时。 (2)态特定(State-specific, SS)：令溶剂直接对指定的激发态的密度进行响应，通过反复迭代令溶剂场与激发态密度间完全自洽。每次迭代都要做电子激发计算求出激发态密度，因而也称外迭代(External iteration)。这将使计算耗时增加一个数量级，还使得TDDFT失去解析梯度。因此仅当对结果要求精确的时候使用，且一般不用在优化激发态的过程中。而且一次只能考虑一个激发态，难以获得同时涉及很多态的吸收光谱。一般来说，除非考察的是电荷转移激发态，否则昂贵、麻烦的SS实际上并不比LR有多大优势，甚至还可能结果更差。

溶质会使溶剂分子被极化，包括溶剂的电子结构被极化以及分子朝向被极化，分别对应于溶剂弛豫的快部分和慢部分。对于处于某个电子态的体系，若溶剂的两部分都已经对其弛豫了，称为平衡溶剂(eq)；如果只是快部分弛豫了，称为非平衡溶剂(neq)。垂直吸收、垂直发射的过程非常短暂，末态时溶剂分子只有其电子部分来得及被重新极化，而朝向来不及被重新极化还停留在初态的状况，因此初态计算时应处于平衡溶剂下，而末态计算时应处于非平衡溶剂下。绝热吸收/发射过程则可认为在初态和末态时溶剂都已完全弛豫，即都处在平衡溶剂下。在溶剂中计算吸收/发射能严格来说应当考虑非平衡溶剂效应（尽管是否考虑影响不很大），根据上面的讨论，计算方法如下所示

垂直吸收能 = E_ES(R_GS, neq) - E_GS(R_GS, eq) 垂直发射能 = E_ES(R_ES, eq) - E_GS(R_ES, neq) 绝热吸收能 = 绝热发射能 = E_ES(R_ES, eq) - E_GS(R_GS, eq)

其中E_ES和E_GS分别代表激发态和基态能量。R_ES和R_GS分别代表激发态极小点结构和基态极小点结构。诸如E_ES(R_GS, neq)的含义就是在基态极小点结构下、非平衡溶剂下的激发态能量。

是否考虑非平衡溶剂效应，用线性响应还是态特定方法，是不同类别的问题，可以以不同方式组合。原理上说，用态特定方法，同时考虑非平衡溶剂效应，得到的激发能是最准确的，但也最耗时、繁琐，Gaussian手册上那个“7步”例子之所以搞得那么麻烦，就是因为用了这种方式考虑溶剂，而且从吸收到发射算了一个完整来回，于是把初学者们搞晕了。如果不要求那么高，用线性响应模型其实就够了，由于误差抵消之类因素，也不一定比态特定的结果差，还省了大量时间。

5. 气相下计算某分子S1结构和荧光发射能

1 基态几何优化：# PBE1PBE/6-311g(d) opt （如果你觉得初始结构已经比较合理的话，这一步可以省） 2 取上一步优化得到的结构，做S1态优化：# PBE1PBE/6-311g(d) TD opt （TD默认是root=1，默认的nstates=3对于优化S1一般够了，所以这里只写个TD）

第二步最后的结构就是S1结构了。每一步优化都会做一次电子激发计算，所以会看到很多上一节那样的输出。最后一次输出的第一激发态的激发能就是荧光发射能了。

利用第二步的输出文件就可以绘制荧光光谱了。这里假定是符合kasha规则从S1发射的，所以绘图时要把一同输出的S2、S3的信息抹掉。如果用gview绘制，手动将S2、S3态的振子强度设为0，再按照绘制UV-Vis光谱操作即得到荧光光谱。若用Multiwfn绘制则不需要手动修改输出文件，将输出文件载入Multiwfn，依次输入以下命令即可 11 //绘制光谱图 3 //UV-Vis 20 //修改振子强度 2,3 //选择第2、3激发态 0 //振子强度设为0 0 //绘制光谱

如果你还有不明白的地方，看Multiwfn手册4.11.11节，里面有个完整的绘制BODIPY荧光光谱的例子。

顺带一提，如果你要优化S4，可以写比如# PBE1PBE/6-311g(d) TD(nstates=7,root=4) opt。

6. T1的优化

优化T1值得专门一说。有两种做法，一种是用UDFT（也叫UKS），即自旋多重度设3直接优化，不写TD关键词，比如0 3结合# PBE1PBE/6-31G* opt，这样是通过SCF方式直接算T1态并优化它，不牵扯TDDFT计算；另一种是自旋多重度设1同时用TD(triplet)，比如0 1结合# PBE1PBE/6-31G* TD(triplet) opt，这样每一步就是先计算单重态基态作为参考态，再通过TDDFT计算T1态并优化它。这两种方式原理上都合理，结果通常相近，但强烈建议用UDFT方式，因为其耗时只比优化单重态基态增加一点，而用TDDFT优化T1的话计算量则要增加约一个数量级。

不过UDFT方法缺点是只能优化T1，而TDDFT则可以优化任意三重态激发态，而且能够同时给出轨道跃迁信息。

经常有初学者写成0 3结合TD(triplet) opt，这样算出来什么都不是，根本就不是优化T1。

7. 气相下计算T1结构和磷光发射能

有两种方法做这个事情。

方法一： 1 优化T1结构：# B3LYP/6-31G* opt，电荷和自旋多重度为0 3。 2 取上一步优化得到的结构，用# B3LYP/6-31G* TD(triplet)，电荷和自旋多重度为0 1。第一激发态的激发能就是磷光发射能了。

方法二： 1 优化T1结构：# B3LYP/6-31G* opt，电荷和自旋多重度为0 3。取最后一步的能量，作为T1结构下T1能量。 2 取上一步优化得到的结构，0 1下用# B3LYP/6-31G*计算单点能，得到T1结构下S0能量。 3 将第1步的能量减去第2步的能量即是磷光发射能

虽然两个方法结果有定量差异，但原理上都对，由于方法二还考虑了轨道弛豫，所以原则上会更精确一些，而且由于不用做TDDFT计算所以耗时短，缺点是没法像方法一那样得到轨道跃迁信息。另外，如果你还用TDDFT算了荧光，那么建议用方法一算磷光，这样都在TDDFT下计算结果更有可比性。

由于Gaussian不支持TDDFT级别下的旋轨耦合计算，所以得不到磷光发射对应的振子强度（输出的数值为0），因此没法绘制磷光光谱、计算磷光速率。支持MCSCF、MRCI等级别下做旋轨耦合的程序不少，不过这类方法很难用于大体系。目前支持TDDFT下考虑旋轨耦合得到振子强度的程序不算多，只有ADF（巨贵而且坑爹，别买）、Dalton（免费，推荐使用，计算例子见http://bbs.keinsci.com/thread-2455-1-1.html，以及计算化学公社量子化学版里面Dalton分类的帖子），以及Dirac等支持二/四分量相对论TDDFT的程序（使用门槛略高）。如果你只需要计算单-三重态间的旋轨耦合矩阵元的话，可以将Gaussian与PySOC结合使用，见《使用Gaussian+PySOC在TDDFT下计算旋轨耦合矩阵元》（http://sobereva.com/411）。更好、更方便的选择是用ORCA，见《使用ORCA在TDDFT下计算旋轨耦合矩阵元和绘制旋轨耦合校正的UV-Vis光谱》（http://sobereva.com/462）。

8. 注意优化激发态时破坏对称性

就是激发态和基态的对称性往往是不同的，优化小分子激发态的时候不注意这一点往往得不到真正的激发态极小点结构。例如乙醛，基态是Cs对称性，但是S1的极小点结构并不具有Cs对称性。因此，直接拿它的基态结构作为初始结构来优化S1是万万不可的，否则得到的S1结构会依然保持Cs对称性，做振动分析会发现虚频。为得到真正极小点结构，应当在优化S1前先把基态的结构人为地扭曲一下使得Cs对称性被破坏，比如随意微微扭动一个二面角。激发态对称性往往低于基态，所以如果基态有对称性，建议激发态优化前都先人为地稍微破坏一下对称性。